曰批一级视频播放,韩日美无码精品无码,国产莉萝无码AV在线播放

通過因果邏輯分析、統計假設檢驗和實驗驗證，可以判斷缺陷產生的原因。

因果分析需要利用現有的知識和信息對假設進行邏輯判斷，并對數據反映的問題進行解釋。比如在郵局，就有很多匯款失敗的情況。假設團隊認為是工作人員在匯款管理過程中出錯造成的，這或許可以解釋一些錯誤，但無法解釋不熟悉填表細節的客戶(老人和小孩)會犯更多錯誤的現象。如果匯款管理系統出現問題，您應該認為對所有客戶的影響都是相似的。因此，假設匯款管理系統是問題的原因，這或許可以解釋看得見的問題(如匯款有缺陷)，但無法解釋看不見的問題:老人和孩子更容易匯款失敗。

為了使假設的理由真的成立，必須通過因果邏輯分析來驗證。當然，一些潛在的問題現在并不明顯。

2、統計假設檢驗

散點圖、相關分析和回歸分析是分析因果關系的常用方法。

通過散點圖可以對原因X和結果Y的關聯程度有一個印象，然后用精確的計算進行相關分析和回歸分析，得到一定的統計模型。在某些情況下，原因和結果根本沒有任何關系。在沒有任何模型的情況下，我們可以通過散點圖得到一些信息。

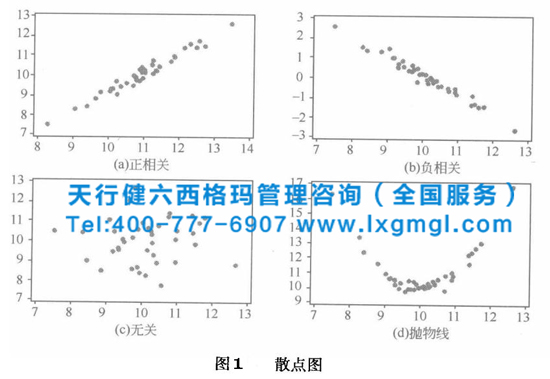
散點圖提供了一種驗證因果假設的方法，從幾對數據中驗證自變量X和因變量Y之間是否存在相關性。配對數據，顧名思義，就是X和Y來自同一個被觀察個體，“配對”本身就反映了兩個變量之間的關系，可能只是表面的相關，也可能是潛在的因果。一般來說，取一批配對數據(X，Y)作為平面坐標系中的橫坐標和縱坐標，就可以形成散點圖，X和Y的相關關系在圖中顯示，如圖1所示。

六西格瑪數據分析的第三階段：驗證結果

如果數據點從左到右呈一定角度分布，如圖1(a)所示，說明自變量X和因變量Y正相關。簡單來說，這個趨勢就是“隨著X的增大，Y趨于增大”。其他類型為負相關，如圖1(b)；不相關，如圖1(c)所示，或者更復雜的相關(在這個例子中，拋物線型，如圖1(d)所示)。

散點圖顯示的強正相關并不能100%保證X的增加一定會導致Y的增加，但確實說明了它們在某種程度上是相互關聯的，同時也不是完全隨機的。相關性并不等同于因果關系。比如企業某段時間內的“工人加班時間”與“生產的不合格產品數量”有很高的相關性，但兩者之間沒有因果關系。關聯度高的真正原因是那段時間生產安排非常集中和緊張，導致工人加班時間和生產的不合格品數量同步增加。因此，團隊在使用散點圖來說明相關性時要小心，但有時確實會發現一些因果關系的結果，所以這種方法還是很有用的。如果考慮兩個以上的變量，相關性分析可能會非常復雜。這時可以將變量分組，兩兩組合，得到多個散點圖，驗證猜測的正確性。您還可以在同一個矩陣散點圖上繪制所有變量的成對數據散點圖，并同時進行分析。

在繪制散點圖之前，可以對數據進行整理、加工、分類，將同一問題的數據按不同類型進行匹配，做出矩陣散點圖。也可以按照不同層次做散點圖，分層分析。并非所有的缺陷都是由相同的背景引起的，在測量階段發現的分類因素可能對確定因果模型過程有用。